Производная суммы функций - одно из фундаментальных правил дифференциального исчисления, позволяющее находить производные сложных выражений. Рассмотрим это правило подробно.
Содержание
Основное правило дифференцирования суммы
Производная суммы двух или более дифференцируемых функций равна сумме их производных:
(f(x) + g(x))' = f'(x) + g'(x)
Формальное доказательство
Используя определение производной через предел:
- Рассмотрим функцию h(x) = f(x) + g(x)
- Найдем предел: h'(x) = limΔx→0 [h(x+Δx) - h(x)]/Δx
- Подставим h(x): = limΔx→0 [f(x+Δx)+g(x+Δx) - f(x)-g(x)]/Δx
- Перегруппируем: = limΔx→0 [f(x+Δx)-f(x)]/Δx + limΔx→0 [g(x+Δx)-g(x)]/Δx
- Получаем: = f'(x) + g'(x)
Обобщение на n функций
Правило распространяется на любое конечное число слагаемых:
(f1(x) + f2(x) + ... + fn(x))' = f'1(x) + f'2(x) + ... + f'n(x)
Примеры вычислений
| Функция | Производная |
| (x2 + sin x) | 2x + cos x |
| (ex + 3x4 + ln x) | ex + 12x3 + 1/x |
| (5x + 7) | 5 + 0 = 5 |
Дифференцирование суммы с коэффициентами
Правило работает и для линейных комбинаций функций:
(a·f(x) + b·g(x))' = a·f'(x) + b·g'(x)
где a и b - постоянные коэффициенты.
Пример:
- Функция: 3x2 - 5cos x
- Производная: 3·2x - 5·(-sin x) = 6x + 5sin x
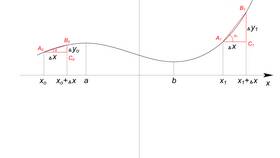
Геометрическая интерпретация
Сумма функций означает сложение их значений по вертикали. Производная, как угловой коэффициент касательной, также складывается:
- Наклон суммы = сумме наклонов
- Касательная к сумме функций = сумме касательных
Применение в физике
Правило часто используется при анализе сложных движений:
| Ситуация | Применение |
| Скорость как производная пути | Скорость суммарного движения = сумме скоростей |
| Ускорение как производная скорости | Результирующее ускорение = сумме ускорений |
Ограничения и особенности
- Функции должны быть дифференцируемы в рассматриваемой точке
- Для бесконечных сумм (рядов) правило применимо только при равномерной сходимости
- Правило не распространяется на произведение функций
Заключение
Правило дифференцирования суммы функций является одним из основных инструментов математического анализа. Его простота и универсальность позволяют эффективно находить производные сложных выражений, разбивая их на более простые компоненты.